Qu’est qu’une prévision statistique ?

Sommaire

I Contexte

I.1 Variable d’intérêt

I.2 Méthode d’échantillonnage

II Prévision d’un effectif

II.1 Distribution des probabilités d’un effectif (loi binomiale)

II.2 Espérance mathématique d’un effectif

II.3 Intervalle de confiance d’un effectif

III Prévision d’une fréquence

III.2 Espérance mathématique d’une fréquence

III.3 Intervalle de confiance d’une fréquence

L’effectif ou la fréquence dont on cherche une prévision dans l’échantillon de taille n, concerne la modalité A d’une variable d’intérêt qualitative. Chaque individu de la population présente la modalité A ou son contraire . La proportion p_pop des individus A dans la population est connue.

I.2 Méthode d’échantillonnage

On prévoit de prélever au hasard dans la population n individus avec remise. Dans ces conditions à chaque prélèvement d’un individu de l’échantillon la proportion de A dans la population reste constante, et par conséquent la probabilité p_pop d’obtenir A, égale à cette proportion, aussi. Mais quand la taille de la population est infinie, le fait de prélever l’échantillon sans remise ne modifie pas non plus les conditions du tirage au fur et à mesure du prélèvement de l’échantillon.

II Prévisions d’un effectif

II.1 Distribution des probabilités d’un effectif (loi binomiale)

Le nombre Y_éch d’individus A dans l’échantillon à l’issue des n tirages (Y est donc une deuxième variable, qui, elle, est quantitative), peut prendre, a priori, les valeurs k = 0, 1, …, k, …, n, avec les probabilités : 

P(Yéch = k) =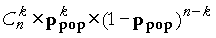

Cette distribution est appelée loi binomiale, et notée B(n ; p_pop).

Exemple de la loi B (n = 350 ; p_pop = 0,0125) :

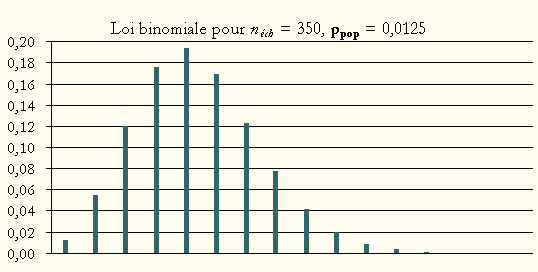
On voit qu’on obtiendra un effectif compris entre 0 et 12. La probabilité d’obtenir un effectif supérieur (qui peut théoriquement aller jusqu’à 350) est négligeable. L’effectif qui a la plus grande probabilité de se produire est 4. La probabilité d’obtenir un effectif de 3 ou 5 est supérieure à celle d’obtenir un effectif de 4.

II.2 Espérance mathématique d’un effectif

L’espérance mathématique de Y_éch est la limite de l’effectif moyen d’individus A parmi les n prélevés si l’on répète indéfiniment le prélèvement de n individus :

Cette espérance mathématique n’est pas forcément une valeur entière (dans l’exemple 4,38).

La valeur entière la plus proche de l’espérance mathématique est celle dont la probabilité de réalisation est la plus grande.

II.3 Intervalle de confiance (I.C.) d’un effectif

L’intervalle de confiance correspondant à un niveau de confiance a donné ne peut être ni aisément, ni exactement calculé. Pour certaines valeurs de n et p_pop, on peut aisément et assez précisément construire une approximation d’un I.C. centré sur l’espérance mathématique en fonction de l’écart-type de la distribution de l’effectif, comme au § IV.2.a).

s(Yéch) =

III Prévision d’une fréquence

III.1 Distribution des probabilités d’une fréquence (loi binomiale)

La fréquence f_éch = de A dans l’échantillon de taille n étant la simple division de l’effectif par la taille de l’échantillon, prend les valeurs 0, , , ... , , ... , , 1, avec les mêmes probabilités que Y_éch pour les valeurs de k.

III.2 Espérance mathématique d’une fréquence

L’espérance mathématique de f_éch est :

III.3 Intervalle de confiance d’une fréquence

L’intervalle de confiance de la fréquence se déduit de celui de l’effectif. La variance et l’écart-type de la fréquence sont :

V(féch) =

s(féch) =

IV Calculs de probabilités dans la loi binomiale

IV.1 Calculs directs

La plupart des calculettes financières ont une touche (2^nd nCr pour la TI BA2+) ou une ^{fonction pour calculer les combinaisons .}.

La fonction d’Excel LOI.BINOMIALE(k ; n ; p ; vrai ou faux) renvoie avec faux la probabilité ponctuelle P(Y=k).
Avec vrai cette fonction renvoie la probabilité cumulée de l’intervalle P(Y £ k).

En pratique on ne calcule des probabilités ponctuelles P(Y=k) que pour des valeurs de k voisines de l’espérance mathématique, et seulement quand cette espérance est faible (n.p_pop < 8 pour fixer les idées).

Pour calculer "à la main" des probabilités ponctuelles, on a intérêt à les enchaîner à partir de k = 0 :

• P(Y = 0) = (1 – p)ⁿ, puis les suivants,
• P(Y = k) = P(Y = k – 1) ´  p/(1 – p) ´ (n – k + 1)/k

Exemple : calcul de P(Y>3) = 1 – P(Y=0) – P(Y=1) – P(Y=2) – P(Y=3) avec n =10, p = 0,2 :

• P(Y=0) = (1 – 0,2)¹⁰,
• P(Y=1) = P(Y=0) ´  0,2/(1 – 0,2) ´  10/1,
• P(Y=2) = P(Y=1) ´  0,2/(1 – 0,2) ´  (10 – 1)/2
• P(Y=3) = P(Y=2) ´  0,2/(1 – 0,2) ´  (10 – 2)/3.

IV.2 Calculs approchés

Le calcul direct s’avère techniquement difficile, voire impossible, même avec un ordinateur lorsque n et k sont grands, à moins que p_pop ne soit très petit. On distingue plusieurs cas.

a) Quand n.p_pop est > 20

Les probabilités ponctuelles P(Y=k) sont toutes faibles, voire négligeables, et ne présentent donc pas d’intérêt. On s’intéresse aux probabilités d’intervalles P(Y £ k) ou P(Y >k) dont on peut calculer une valeur approchée avec la loi de Gauss de même moyenne m = et écart-type .

Mais il faut parfois faire une correction de continuité car, dans la loi binomiale, P(Y£k) = P(Y<k+1), alors que dans la loi de Gauss ces deux valeurs peuvent être d’autant plus différentes que n..p_pop est faible.

Approximation de l’intervalle de confiance. En fonction de niveau de confiance a, l’intervalle de confiance, dans la loi de Gauss est, pour l’effectif :

n.ppop - ta £ Yéch £ n.ppop + ta

et, pour la fréquence :

ppop - ta £ féch £ ppop + ta

Avec les principales valeurs :

b) Quand n.p_pop est < 20

Quand n.p_pop est peu différent de n.p_pop.(1 – p_pop), on peut obtenir une valeur approchée de P(Y=k) ou de P(Y £ k) par lecture de la table de la loi de Poisson de paramètre n.p_pop.

V Prévision d’un effectif d’un échantillon sans remise d’une population finie

On parle aussi de tirage "exhaustif". On tire simultanément n individus parmi N. Ceci revient à prélever successivement mais sans remise l’échantillon. Il y a toujours, au départ, la proportion p_pop d’individus A parmi les N. Mais, évidemment, cette proportion fluctue de façon aléatoire au fur et à mesure du prélèvement de l’échantillon, c’est-à-dire que p(A) dépend à chaque prélèvement des résultats des prélèvements précédents.

V.1 Distribution des probabilités des effectifs (loi hypergéométrique)

La prévision de Y_éch est une loi hypergéométrique de moyenne n.p_pop (inchangée par rapport à l’espérance mathématique de la loi binomiale) et de variance n.p_pop.(1 – p_pop)..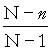

V.2 Approximation de la loi hypergéométrique

L’approximation par la loi de Gauss n’est plus possible, ni la prévision par intervalle de confiance de Gauss, sauf quand le taux de sondage () est faible (en pratique < 10%), et que p_pop (ou 1 – p_pop ) n’est pas trop petit. On peut alors écrire :

P(p_pop - t_a £ f_éch £ p_pop + t_a) = a

Retour à la page d’acceuil

Autres fiches de statistique

Qu’est qu’une prévision statistique

Retour en haut de la page

Erreurs, omissions, remarques ?