Qu'est qu'une prévision statistique ?

Sommaire

I Contexte

I.1 Variable d'intérêt

I.2 Méthode d'échantillonnage

II Prévision du total Y_éch

III Prévision de la moyenne m_éch

IV Prévision de l'écart-type s_éch

V Intervalle de confiance d’une moyenne d’échantillon pour le niveau de confiance

Retour à la page d'acceuil

Autres fiches de statistique

I Contexte

I.1 Variable d'intérêt

Le total ou la moyenne dont on cherche à prévoir la valeur dans un échantillon au hasard de taille n concerne une variable d'intérêt quantitative continue, qu'on appelle Y. On note Y_éch ce total, m_éch cette moyenne . On note s_éch l’écart-type de Y dans l'échantillon.

La moyenne et l'écart-type s_pop de Y dans la population sont connus.

Par contre la distribution L(Y) de Y dans la population n'est pas forcément connue. Le cas d'une distribution de Gauss dans la population est courant.

I.2 Méthode d'échantillonnage

On prévoit de prélever au hasard et avec remise n individus dans la population.

II Prévision du total Y_éch

La distribution des probabilités dépend de la distribution de Y dans la population.

Quand la distribution de Y dans la population est de Gauss, L(Y) = N (; s_pop), la distribution du total Y_éch de l'échantillon au hasard avec remise est alors aussi de Gauss :

L(Y_éch)= N (n. , s_pop´ ).

Dans tous les cas, son espérance mathématique est n ´, sa variance n ´ s²_pop, et son écart-type s_pop´ .

III Prévision de la moyenne m_éch

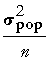Les résultats sont similaires aux précédents. La distribution des probabilités de la moyenne dépend de la distribution de Y dans la population. Elle a pour espérance mathématique , pour variance , et pour écart-type . Cette moyenne est une prévision ponctuelle de la moyenne de l'échantillon.

Quand la distribution de Y dans la population est de Gauss, la distribution de la moyenne m_éch de l’échantillon au hasard avec remise est alors aussi, quelque soit sa taille n, de Gauss.

Dans le cas contraire, la distribution de la moyenne m_éch tend vers une loi de Gauss quand la taille de l'échantillon au hasard avec remise tend vers l'infini (théorème de la limite centrale). En pratique, dés que n >15 à 20, l’approximation est suffisante.

IV Prévision de l'écart-type s_éch

La distribution des probabilités dépend de la distribution de celle de Y dans la population. Son espérance mathématique est s _pop ´ .

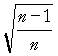V Intervalle de confiance d’une moyenne d’échantillon au hasard

V.1 Echantillon avec remise dans une population Gaussienne

Quand la distribution de Y dans la population est de Gauss (ou peut être ajustée par une loi de Gauss) N (; s_pop), et que l'échantillon est au hasard avec remise, l'intervalle de confiance au niveau de confiance a est :

P( – t_a  £ m_éch £  + t_a ) = a

avec t lu dans la table de la loi de Gauss en fonction de a :

V.2 Grand échantillon avec remise dans une population non Gaussienne

Quand la distribution de Y dans la population n’est pas de Gauss, ou, ne peut pas être ajustée par une loi de Gauss le théorème de la limite centrale affirme que le résultat précédent n'est vrai que lorsque la taille de l'échantillon n tend vers l'infini. Mais la convergence est très rapide, et dés que n est grand, en pratique dés que n > 15, le résultat précédent s'applique.

V.3 petit échantillon avec remise dans une population non Gaussienne

Pour un petit échantillon on peut appliquer le théorème de Bienaymé-Chebitchef :

P( – (1 – a )^– ¹^/²  £ m_éch £ + (1 – a )^– ¹^/² ) = a

V.4 échantillon sans remise dans une population Gaussienne ou non

Quand l’échantillon au hasard est sans remise, la loi de sa moyenne n’est plus, ni ne tend plus vers une loi de Gauss. Sa moyenne est toujours . Sa variance est multipliée par le coefficient d’exhaustivité . On admet que, lorsque le taux de sondage () est inférieur à 10%, on peut encore utiliser la loi de Gauss, et écrire :

P( – t_a   £ m_éch £  + t_a ) = a

avec t lu, comme plus haut, dans la table de la loi de Gauss en fonction de a.

Retour à la page d'acceuil

Autres fiches de statistique

Qu'est qu'une prévision statistique

Retour en haut de la page

Erreurs, omissions, remarques ?

Dernière mise-à-jour de cette page : jeudi 01 février 2001.