inconnue de la moyenne d’une variable d’intérêt Y quantitative continue dans une population avec un échantillon au hasard. L’écart-type de Y dans la population est spop. La distribution de Y n’est pas précisée.| Estimation d’une moyenne par échantillon au hasard |
Qu'est-ce qu'une estimation statistique
On cherche à estimer la valeur inconnue de la moyenne d’une variable d’intérêt Y quantitative continue dans une population avec un échantillon au hasard. L’écart-type de Y dans la population est spop. La distribution de Y n’est pas précisée.
Que l’échantillon au hasard ait été tiré avec ou sans remise :
|
|
où méch désigne la moyenne arithmémtique observée, c'est-à-dire calculée dans l'échantillon.
III Estimation par intervalle de confiance
III.1 Echantillon au hasard avec remise
a) Cas où la distribution de Y peut être ajustée par une loi de Gauss
Ce cas peut, par exemple, résulter d’un test de la droite de Henry sur papier Gausso–arithmétique.
Alors :
|
P(méch ta ´ |
où
b) Cas où la distribution de Y ne peut pas être ajustée par une loi de Gauss
Le résultat est le même que ci-dessus, mais seulement quand l’échantillon est grand (en pratique n > 5, d’après le théorème de la Limite Centrale).
c) Cas où spop est connu
Les deux résultats ci-dessus sont respectivement remplacés par :
|
P(méch – ta
´
|
où ta est lu dans la table de la loi de la loi de Gauss.
L’écart-type de l’estimation de la moyenne est modifiée d’un "coefficient d’exhaustivité" :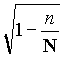 
.
Attention : Ce coefficient d’exhaustivité n’est pas le même que celui de la prévision de la moyenne ou de la fréquence d’un échantillon au hasard exhaustif.
Il n’est théoriquement plus possible d’utiliser la loi de Gauss pour calculer l'intervalle de confiance.
On peut utiliser le théorème de Bienaymé – Tchébicheff.
Erreurs, omissions, remarques ?
Dernière mise-à-jour de cette page : mardi 7 février 2001.
= méch
< 
<