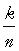Test graphique d’ajustement d’une distribution à une loi de Gauss
(droite de Henry)

Qu’est-ce qu’un test statistique

I Hypothèse de normalité testée

On cherche à vérifier si, dans la population à laquelle on s’intéresse, la distibution d’une variable quantitative Y peut être ajustée par une loi de Gauss. La connaissance de l’espérance mathématique et de l’écart-type de la loi n’est pas nécessaire.

II Statistique d’échantillon étudiée

Le test de la droite de Henry porte sur la courbe des fréquences cumulées d’un n-échantillon au hasard extrait de la population dans laquelle on veut vérifier si la distribution de Y est Gaussienne, tracée sur un papier graphique spécial dit "papier Gausso-arithmétique" :

III Réalisation du test

Chaque point tracé sur le graphique a :

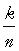  • Pour abscisse une valeur y observée de la variable d’intérêt.
  • Pour ordonnée la fréquence cumulée correspondante observée dans l’échantillon , ,où k est l'effectif des individus de l'échantillon qui ont une valeur inférieure ou égale à la valeur y.

    • On trace à la main autant de points que l’on souhaite.

    IV Interprétation du test

    Si la distribution de la variable dans l’échantillon était de Gauss, les points seraient parfaitement alignés. Si la distribution de la variable dans la population est de Gauss, la courbe obtenue avec la distribution de l’échantillon, qui n’a aucune raison d’être de Gauss, devrait tout de même, puique l’échantillon est au hasard, être voisine d’une droite, et ceci d’autant plus que cet échantillon est grand.

    Par conséquent :

  • Si les points obtenus sont sensiblement alignés, on conclut qu’il n’y a aucune raison de rejeter l’hypothèse de normalité dans la population.
  • Si les points obtenus ne sont pas sensiblement alignés, on conclut qu’on rejete l’hypothèse de normalité dans la population.

    • Le jugement est, évidemment, totalement subjectif, et le test est assez "rustique".

    V Estimation graphique des paramètres de la distribution de Gauss

    Quand on conclut à la normalité de la distribution, la droite qui ajuste le mieux le nuage des points tracés représente la loi de Gauss qui ajuste la distribution statistique de la variable d’intérêt dans la population. On peut alors estimer graphiquement :

  • Sa moyenne, par sa médiane, à l’abscisse de l’intersection de la droite avec l’horizontale à la fréquence de 50%.
  • Son écart-type par la demie amplitude de l’intervalle des abscisses de.ses intersections avec les horizontales aux fréquences de 0,1587 et 0,8413 (en pointillés sur le graphique).

    • Retour en haut de la page

    Autres fiches de statistique

    Retour à la page d’ accueil

    Erreurs, omissions, remarques ?

    Dernière mise-à-jour de cette page : mardi 16 janvier 2001 09:02:28.